novembre 2010 - MeDiaN@Tour

2010
11.28

MeDiaN@Sports – « L’Aérodynamisme à vélo »

Catégorie: .MeDiaN@Sports / Tags: aucun tag / 2 commentaires

Présentation générale

Dans ce précédent article, nous avons vu que l’équation gérant le mouvement d’un cycliste peut s’écrire sous la forme suivante :

$C_{m} = K\ddot{\theta_{p} } + \left ( \lambda_{1}+2. \lambda_{2}t \right ) \dot{\theta_{p}} + \left (M_{tot} \right ) .g.a.t.sin(\alpha)$
Avec $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$
$M_{tot} = \left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste} \right )$
$\alpha = Arctan (\frac{Denivele}{100})$
$t=\frac{Ndents_{plateau} }{Ndents_{pignon}}$

Cette équation est cependant insuffisante pour représenter la réalité car elle néglige l’ensemble des actions extérieures s’opposant pourtant à l’avancement du cycliste. Pour obtenir une modélisation plus précise, il faudra donc prendre en compte un certain nombre d’actions supplémentaire et en particulier celles dues à l’air.

Résistance aérodynamique

Pénétration dans l’air

Modélisation mathématique

La résistance aérodynamique est l’action exercée par l’air sur le cycliste lorsque celui-avance. Pouvant être favorable ou défavorable, sa valeur est proportionnelle au carré de la vitesse relative du cycliste par rapport au vent.

Bien que la détermination précise des phénomènes aérodynamique soit extrêmement complexe, on peut cependant obtenir une idée de cette résistance grâce à la formule ci-dessous:

$R_{C_{x}}= \frac{1}{2}.\rho .S.C_{x}.V^{2}_{a}= \frac{1}{2}.\rho .S.C_{x}.(V_{vent}+\dot{\xi })^{2}$
avec $\rho$ la masse volumique de l’air;
$S$ la surface frontale du cycliste;
$C_{x}$ le coefficient de pénétration dans l’air du cycliste (environ 0.9);
et $V_{vent}$ vitesse du vent est comptée positivement lorsqu’il est opposé à la vitesse d’avancement

Paramètres influents 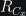$R_{C_{x}}$

Les conditions atmosphériques (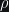 $\rho$ )

La masse volumique de l’air dépend de plusieurs facteurs qui sont l’humidité, la température et la pression atmosphérique qui varie avec l’altitude. Dans les conditions normales, on peut approcher la masse volumique de l’air grâce à la formule suivante :

$\rho (H_{g} ,\theta, p )=\frac {1} {287,06 (\theta +273,15)} (p - 230,617.H_{g} . exp(\frac{17.5043.\theta}{241.2+\theta }))$

A 20°C et à pression normale, on considère souvent que $\rho_{20}=1.204kg/m^3$

La taille et la position du cycliste, la géométrie de son matériel ( $S et C_{x}$ )

Le $C_{x}$ est le coefficient de pénétration dans l’air de l’ensemble Cycliste+Vélo. Il diffère suivant la position du cycliste et l’incidence du vent. Cependant, on peut considérer que 0,95 est une bonne approximation de ce coefficient dans la majorité des cas.

S est la surface frontale de l’ensemble cycliste+Vélo. Cette surface peut être déterminée assez facilement en utilisant un appareil photo numérique et le logiciel The Gimp (voir ce tuto). Voici ce que l’on obtient dans mon cas.

On peut aussi noter que les positions en contre la montre et/ou des tri-athlètes permettent d’atteindre des SCx de l’ordre de 0,25.

Du vent apparent

Le vent apparent est la vitesse du vent par rapport au cycliste. Il dépend de la vitesse propre du vent, de son incidence et de la vitesse du cycliste.

Ainsi, $V_{a}^{2}=(V_{vent}. cos(i)+V{Cycliste})^{2}=(V_{vent}.cos(i)+\dot{\xi })^{2}$

Conclusion

La résistance dû à l’air ramenée au pédalier est finalement donnée par la relation :

$R_{C_{x}}= \frac{1}{2}.\rho .S.C_{x}.(V_{vent}.cos(i)+a.t.\dot{\theta_{p}})^{2}$

Friction de l’air

Lorsque qu’un vélo avance, le frottement de l’air sur celui-ci ainsi que les phénomène aérodynamique qu’il génère (traînée, dépression,…) agissent comme un frein à cet l’avancement. L’essentiel de ces pertes sont en réalité générées par la rotation des roues et c’est pourquoi les fabricants proposent de plus en plus des roues dites aérodynamique (jantes hautes, réduction du nombre de rayons, rayons profilés,…).

Ces roues peuvent alors être caractérisées par un coefficient qui définit leur efficacité de friction (Cf=0.0027 pour des roues standards avec des pneus 700x23C).

La résistance due à la friction de l’air peut être approximée grâce à la relation ci-dessous :

$R_{friction_{air}}= C_{f}.(V_{vent}.cos(i)+a.t.\dot{\theta_{p}})^{2}$

Conclusion

La prise en compte de l’aérodynamisme nous permet d’accroître la précision de l’équation du mouvement établie précédemment. Celle ci devient désormais :

$C_{m} = K\ddot{\theta_{p} } + \left ( \lambda_{1}+2. \lambda_{2}t \right ) \dot{\theta_{p}} + \left (M_{tot} \right ) .g.a.t.sin(\alpha) + C_{aero_{p}}$
Avec $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$
$M_{tot} = \left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste} \right )$
$\alpha = Arctan (\frac{Denivele}{100})$
$t=\frac{Ndents_{plateau} }{Ndents_{pignon}}$
$C_{aero_{p}}=t.C_{aero_{roues}}=a.t.R_{aero}$
$R_{aero}=R_{C_{x}}+R_{friction_{air}}=(\frac{1}{2}\rho.S.C_{x}+C_{f}).(V_{Vent}.cos(i)+a.t.\dot{\theta_{p}})^{2}$

Mais aspirons à aller plus loin…

Tout cycliste ayant déjà rouler en groupe a pu constater l’importance de l’aspiration aérodynamique dans ce sport. Le placement dans un peloton et la capacité du coureur à s’abriter dans les roues permet ainsi une économie énergétique importante non négligeable qui pourra faire la différence en fin de parcours. La littérature fait ainsi souvent état d’un gain possible de 30% en fonction des conditions.

L’objectif de ce paragraphe est de faire apparaître un facteur de correction $k_{corr}$ dans l’équation qui prendra en compte l’aspiration dont pourra profiter le cycliste lors d’une cyclosportive par exemple.

L’idée étant d’affiner le résultat sans dispositif autre que le compteur, la détermination du coefficient correcteur se fera sur la base du raisonnement ci-dessous :
– Le gain maximum attribuer à l’aspiration est d’environ 30%. Nous pouvons donc supposer qu’une sortie en groupe réaliser à 100% dans les roues permet au coureur de réduire de 30% l’énergie dépensée pour vaincre les forces aérodynamiques.
– A l’inverse, un sortie à 2 où les cyclistes prennent les relais à part égale permettra à chacun de s’abriter 50% du temps seulement.

Le facteur correcteur $k_{corr}$ est donc fonction du temps passer à s’abriter par rapport au temps totale de la sortie et pourra s’écrire :

$k_{corr} = 1-\frac{t_{abrite}}{100}*0.3$ où $t_{abrite}$ est le pourcentage de temps passé dans les roues.

Par conséquent, si $t_{abrite} = 100$ %, $k_{corr} = 0.7$
si $t_{abrite} = 0$ %, $k_{corr} = 1$

L’équation tenant compte de l’aspiration est donc :

$C_{m} = K\ddot{\theta_{p} } + \left ( \lambda_{1}+2. \lambda_{2}t \right ) \dot{\theta_{p}} + \left (M_{tot} \right ) .g.a.t.sin(\alpha) + k_{corr}.C_{aero_{p}}$

Cette équation nous permet d’écrire quelques remarques intéressantes :

La résistance aérodynamique varie suivant le carré de la vitesse. Cette résistance augmente par conséquent avec la vitesse de façon exponentielle. L’aspiration pouvant permettre de réduire ces pertes de 30%, il est primordiale de savoir s’abriter correctement lors d’une sortie en groupe pour maximiser ses performances.

Lorsque le vent nous arrive de coté (i=90° ou i=270°), sa participation à la résistance à l’avancement est théoriquement nulle puisque cos(i)=0. Si i est entre 90° et 270°, cos(i)<0 : le vent devient moteur.

La position du cycliste sur son vélo est fondamentale : le fait de passer d’une position bras tendu à une position aéro permet en effet de réduire son SCx de près de 24% ( $\frac{(0.41-0.31)}{0.41}*100$ ) et de réduire d’autant les pertes aéro.

Les conditions climatiques ne sont pas sans incidence sur les pertes aérodynamique.En effet celles-ci sont d’autant plus faibles que la température est élevée, que la pression est faible (altitude) et que le taux d’hygrométrie est grand.

2010
11.10

Mauvaise pioche

Catégorie: Montage / Tags: aucun tag / Commentaires fermés

2010
11.06

MeDiaN@Sports – « L’Equation de mouvement à vélo »

Catégorie: .MeDiaN@Sports / Tags: aucun tag / 1 commentaire

Présentation générale

Dans cet article précédent, nous avons établis la relation donnant l’énergie cinétique d’un cycliste se déplaçant en ligne droite.

Rappel : $T = \frac{1}{2} . K . \dot{\theta _{p}^{2}}=\frac{1}{2} . K \left (\frac{\pi . N}{30} \right)^{2}$ avec inertie équivalente ramenée au pédalier $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$

En se basant sur le résultat de ce calcul, nous allons maintenant cherché à établir grâce aux multiplicateurs de Lagrange l’équation du mouvement régissant le déplacement de ce même vélo le long d’une pente.

Modélisation du problème

Schématisation

Description

Un vélo de centre de gravité G (en $[\xi , \nu, 0])$ avance le long d’une pente formant un angle $\alpha$ avec l’horizontale dans les mêmes conditions que celles énoncées dans l’article précédent.

Résolution

Equation de liaison

$\dot{\theta _{1}}=\dot{\theta _{2}}=\frac{-\dot{\xi }}{a}=\dot{\theta_{p}}.t=\frac{\pi .N.t}{30}$

Calcul des multiplicateurs de Lagrange : Qi

Comme tous les paramètres dépendent de $\theta_{p}$ , on exprimera tous les multiplicateurs en fonctions de cette même variable pour simplifier les dérivations à venir.

Pesanteur :
- Pour le cadre : $\vec{O_{o}G^{\prime}} = \vec{OG}+\vec{GG^{\prime}}=\xi.\vec{xo}+\mu.\vec{yo}+b.\vec{x}+c.\vec{y}$ et comme ( $\vec{x}//\vec{xo}$ ), $\vec{O_{o}G^{\prime}}=\left (\xi+b \right )\vec{xo}+\left (\mu+c\right )\vec{yo}$ .
  Dans Rg, on a
  $\vec{xo}=cos(\alpha).\vec{X0}+sin(\alpha).\vec{Yo}$ et $\vec{yo}=-sin(\alpha).\vec{X0}+cos(\alpha).\vec{Yo}$ .
  Donc
  $\vec{O_{o}G^{\prime}}.\vec{Yo} = \left (\xi+b \right ).sin{(\alpha)}+\left (\mu+c\right ).cos{(\alpha)}$
  Finalement
  $V_{cadre} =M.g . \left [ \left (\xi+b \right ).sin{(\alpha)}+\left (\mu+c\right ).cos{(\alpha)} \right ]+C^{te}$
  et en fonction de $\theta_{p}$ :
  $V_{cadre} =M.g . \left [ \left (a.t.\theta_{p}+b+k \right ).sin{(\alpha)}+\left (\mu+c\right ).cos{(\alpha)} \right ]+C^{te}$
  
  Coefficient de Lagrange : $\left (Q_{cadre}\right )_\theta= -\frac{\partial V_{cadre} }{\partial \theta }=-M.g.a.t.sin{\alpha }$
- Pour la roue avant : $\vec{O_{o}O_{1}} = \vec{OG}+\vec{GO_{1}}=\xi.\vec{xo}+\mu.\vec{yo}+d.\vec{x}+e.\vec{y}$
  De la même façon : $\left (Q_{Rav}\right )_\theta= -\frac{\partial V_{Rav} }{\partial \theta }=-M_{1}.g.a.t.sin{\alpha }$
- Pour la roue arrière : $\left (Q_{Rar}\right )_\theta= -\frac{\partial V_{Rar} }{\partial \theta }=-M_{2}.g.a.t.sin{\alpha }$
- Pour le pédalier : $\left (Q_{Pedalier}\right )_\theta= -\frac{\partial V_{Pedalier} }{\partial \theta }=-\left (m_{P}+2m_{p}\right ) .g.a.t.sin{\alpha }$
- Pour le cycliste : $\left (Q_{Cycliste}\right )_\theta= -\frac{\partial V_{Cycliste} }{\partial \theta }=-M_{Cycliste}.g.a.t.sin{\alpha }$
Finalement, $\left (Q_{Pesanteur}\right )_\theta= -\frac{\partial V_{total} }{\partial \theta }=-\left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste}\right ) .g.a.t.sin{\alpha }$
Actionneurs :
Finalement : $\left (Q_{cycliste/pedalier}\right )_\theta= -\frac{\partial P_{(cycliste/pedalier)}^{*} }{\partial \theta^{*} }=C_{m}-\lambda_{1} \dot{\theta_{p}}$
Liaisons : Les roulements constituant les moyeux des roues n’étant pas parfaits, il conduisent à des pertes par frottement. Comme ci-dessus, elles sont directement proportionnelles à la vitesse de rotation des roues à un facteur $\lambda_{2}$ près. On a donc :
$\left (Q_{moyeu_{roues}}\right )_\theta= -\frac{\partial P_{(moyeu_{roues})}^{*} }{\partial \theta^{*} }=-2. \lambda_{2} \dot{\theta_{1}}=-2. \lambda_{2} \dot{\theta_{p}}.t$

Bilan
$\left (Q_{Systeme}\right )_\theta = \left (Q_{Pesanteur}\right )_\theta + \left (Q_{cycliste/pedalier}\right )_\theta + \left (Q_{moyeu_{roues}}\right )_\theta$
$\left (Q_{Systeme}\right )_\theta = -\left (M_{tot} \right ) .g.a.t.sin(\alpha) + C_{m}-\lambda_{1} \dot{\theta_{p}} - 2. \lambda_{2} \dot{\theta_{p}}t$

Détermination de l’équation générale du mouvement

$\left (Q_{Systeme}\right )_\theta = \frac{\mathrm{d} }{\mathrm{d} t}\left ( \frac{\partial T}{\partial \dot{\theta_{p}}} \right )-\frac{\partial T}{\partial \theta_{p}}$ avec $\frac{\partial T}{\partial \dot{\theta_{p}}} = K \dot{\theta_{p}}$ et $\frac{\partial T}{\partial \theta_{p}} = 0$
D’où $\left (Q_{Systeme}\right )_\theta = K\ddot{\theta_{p} } - 0$
Finalement $-\left (M_{tot} \right ) .g.a.sin(\alpha) + C_{m}-\lambda_{1} \dot{\theta_{p}} - 2. \lambda_{2} \dot{\theta_{p}}t = K\ddot{\theta_{p} }$

Conclusion
$C_{m} = K\ddot{\theta_{p} } + \left ( \lambda_{1}+2. \lambda_{2}t \right ) \dot{\theta_{p}} + \left (M_{tot} \right ) .g.a.t.sin(\alpha)$
Avec $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$
$M_{tot} = \left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste} \right )$
$\alpha = Arctan (\frac{Denivele}{100})$
$t=\frac{Ndents_{plateau} }{Ndents_{pignon}}$

Le couple moteur que doit fournir le cycliste à vitesse constante en cote ( $\ddot{\theta_{p} }=0$ ) doit compenser l’effet de la pesanteur (qui sera d’autant plus important que la masse du cycliste+vélo sera élevée et la pente accentuée) ainsi que les différentes pertes dans la transmission et les roulements.

On constate également que l’inertie intervient quand à elle dès que le cycliste cherche à accélérer sa vitesse. Un vélo à faible inertie favorisera donc particulièrement les changements de rythme.

La vitesse maximale que l’on pourrait calculer à partir de cette équation serait toutefois gigantesque car l’équation ne prend absolument pas en compte l’action qu’exerce l’environnement sur le cycliste (résistance au roulement, facteurs aérodynamique,…).