MeDiaN@Sports - « La Résistance au Roulement à vélo »

2011
01.09

MeDiaN@Sports – « La Résistance au Roulement à vélo »

Catégorie: .MeDiaN@Sports / Tags: aucun tag / Ajouter un commentaire

Présentation générale

Dans ce précédent article, nous avons vu que l’équation gérant le mouvement d’un cycliste peut s’écrire sous la forme suivante :

$C_{m} = K\ddot{\theta_{p} } + \left ( \lambda_{1}+2. \lambda_{2}t \right ) \dot{\theta_{p}} + \left (M_{tot} \right ) .g.a.t.sin(\alpha) + k_{corr}.C_{aero_{p}}$
Avec $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$
$M_{tot} = \left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste} \right )$
$\alpha = Arctan (\frac{Denivele}{100})$ ou $sin(\alpha) = \frac{Denivele_{tot}}{Distance_{tot}}$
$t=\frac{Ndents_{plateau} }{Ndents_{pignon}}$
$k_{corr} = 1-\frac{t_{abrite}}{100}*0.3$
$C_{aero_{p}}=t.C_{aero_{roues}}=a.t.R_{aero}$
$R_{aero}=R_{C_{x}}+R_{friction_{air}}=(\frac{1}{2}\rho.S.C_{x}+C_{f}).(V_{Vent}.cos(i)+a.t.\dot{\theta_{p}})^{2}$

Cette équation nous donne la valeur du couple que le cycliste doit fournir pour rouler à une vitesse donné, et ce en prenant en compte les différentes masses en mouvement, les pertes dans les liaisons, le profil de la route ainsi que l’aérodynamisme globale du système. Pour tous ceux qui ont déjà roulé à vélo, il existe un dernier aspect non moins fondamental à considérer : la résistance au roulement.

Résistance au roulement

De nombreuses relations ont successivement été formulées pour décrire au mieux la résistance au roulement. Bien que les plus complètes fassent intervenir la vitesse dans le calcul, nous nous contenterons dans notre cas de la forme sa plus simple.

L’adhérence nécessaire au roulement d’un pneumatique sur le sol génère une force opposée au mouvement qui est proportionnelle au poids du système (vélo + cycliste) selon un coefficient Crr. Ce coefficient dépend :

Des pneumatiques utilisés

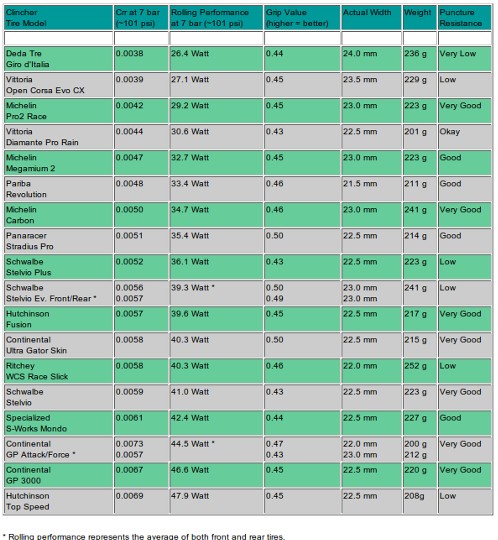
Tous les pneumatiques ne sont pas comparables du point de vue de leur résistance au roulement. Le tableau ci-dessous donne la valeur du Crr à 7bars pour différents modèles de pneus, dont celui des « Michelin Carbon ».

De la pression de gonflage

La résistance au roulement évolue également en fonction de la pression de gonflage. On retrouve souvent cette évolution caractérisée par la fonction suivante : $Crr = Coef_{pneu}*p^{-0.426}$ ou $Coef_{pneu}$ dépend du pneu et p est la pression de gonflage.

Si l’on considère un pneu Michelin Krylion Carbon 700×23 par exemple, on a Crr à 7bars = 0.005. On en déduit que $Coef_{Krylion} = \frac{Crr}{p^{-0.426}}=\frac{0.005}{7^{-0.426}}=0,011454649$

Pour ces pneus, on peut donc donc écrire Crr comme ceci : $Crr_{Krylion} = 0.011454649*p^{-0.426}$

De l’état de la chaussée

L’état de la chaussée joue également un grand rôle sur la mesure du coefficient de roulement. Les valeurs trouvées dans la littérature vont ainsi de 0,004 pour la piste à 0,010 pour une route en asphalte en mauvais état. Pour un route en asphalte très lisse – que l’on peut considérer comme le cas retenu par les fabricants lorsqu’ils nous donnent les caractéristiques de leur pneus – la valeur du Crr est de 0,006.

On peut donc considérer que le Crr varie entre 1*Crr (bonne route) et 1.65*Crr (route dégradée) suivant l’état du revêtement.

$Crr = Coeff_{route}*Coef_{pneu}*p^{-0.426}$ avec $1<Coeff_{route}<1.65$

En considérant que l’on roule les 2/3 du temps sur des routes correctes, la formule retenue pour les Krylion Carbon sera finalement la suivante :

$Crr_{Krylion} = 1.20*0.011454649*p^{-0.426}=0,013745579*p^{-0.426}$

Bilan

La résistance au roulement est finalement donnée par la relation

$Rr=Crr.M_{tot}.g.cos(\alpha)$ avec $\alpha=Arctan(\frac{Denivele}{100})$

Conclusion

L’équation du mouvement qui tient compte de la résistance au roulement est donc :

$C_{m} = K\ddot{\theta_{p} } + \left ( \lambda_{1}+2. \lambda_{2}t \right ) \dot{\theta_{p}} + \left (M_{tot} \right ) .g.a.t.sin(\alpha) + k_{corr}.C_{aero_{p}} + C_{r_{p}}$

Avec $K=a^{2}.t^{2} \left ( M+2. \left (M_{1}+M_{2} \right) + m_{P} + 2. m_{p}+M_{Cycliste} \right)+0,13^{2} \left (m_{P} + 2. m_{p} \right)$
$M_{tot} = \left (M+M_{1}+M_{2}+m_{P}+2m_{p}+M_{Cycliste} \right )$

$\alpha = Arctan (\frac{Denivele}{100})$ ou $sin(\alpha) = \frac{Denivele_{tot}}{Distance_{tot}}$
$t=\frac{Ndents_{plateau} }{Ndents_{pignon}}$

$k_{corr} = 1-\frac{t_{abrite}}{100}*0.3$
$C_{aero_{p}}=t.C_{aero_{roues}}=a.t.R_{aero}$
$R_{aero}=R_{C_{x}}+R_{friction_{air}}=(\frac{1}{2}\rho.S.C_{x}+C_{f}).(V_{Vent}.cos(i)+a.t.\dot{\theta_{p}})^{2}$

$C_{r_{p}}=t.C_{r_{roues}}=a.t.R_{r}$
$R_{r}=Crr.M_{tot}.g.cos(\alpha)$ Avec $Crr = Coeff_{route}*Coef_{pneu}*p^{-0.426}$
avec $cos(\alpha)^{2}+sin(\alpha)^{2}=1$ d’où $cos(\alpha)=\sqrt{1-sin(\alpha)^{2}}$

Ceci nous permet quelques remarques intéressantes:

La résistance au roulement est bien évidemment directement liée à la qualité du pneumatique utilisé et à l’état de la route sur laquelle le cycliste circule.

D’après l’expression du coefficient de résistance au roulement, il est très important de gonflé correctement ses pneus avant chaque sortie. Pour des Krylion Carbon par exemple, le passage de 5 (Crr=0.00692) à 7bars (Crr=0.006) se traduit par une résistance à l’avancement diminuée d’environ 13%.

La surface du pneu en contact avec le sol n’intervient paradoxalement pas dans la relation.

Celle ci dépend en fait de la masse cumulée du cycliste et de son vélo.