La poussée d'Archimède 


Tous les ballons utilisent le « Théorème D’ARCHIMEDE » appliqué dans l'air : "Tout corps immergé dans un fluide subit une force opposée au poids du fluide déplacé".

On nomme cette force "portance aérostatique":

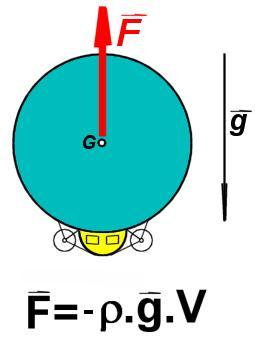
Schéma_poussée_d'Archimède

F : Valeur de la portance (dirigée vers le haut) [N].
G (point d'application): centre de gravité G de l'air déplacé
Ρ : masse volumique de l'air déplacé par le ballon [kg/m3]
V : volume d'air déplacé par le ballon (en vert) [m3]
g : accélération due à la gravité (dirigée vers le bas) [m/s2]


La portance a une valeur numérique très faible. De plus, on n'en exploite qu'un certain pourcentage, puisqu'il faut soulever le ballon lui-même, ses équipements, la motorisation éventuelle, le carburant, le lest, (etc.) avant de soulever la moindre charge marchande. Cette faiblesse a une incidence directe sur la traînée et le coût de l'appareil (énormité des surfaces mouillées). La grande taille est donc la caractéristique essentielle d'un dirigeable (ou ballon).

La portance diminue avec l'altitude. Plus l’altitude est basse, plus la portance est grande. Par exemple :
À 3 km d'altitude : 75 % de la valeur au niveau de la mer. F = 0,9 daN par m3 de ballon
À 6,5 km d'altitude : 50 % de la valeur au niveau de la mer. F = 0,6 daN par m3 de ballon
À 10 km d'altitude : 33 % de la valeur au niveau de la mer. F = 0,39 daN par m3 de ballon

La portance croît comme le volume. Et non comme la surface (cas des aérodynes), ce qui favorise encore plus cette grande taille et interdit pratiquement l'existence des petits ballons.

La portance diminue avec la masse volumique (ρ). Il est donc illusoire de vouloir réaliser des dirigeables pour un usage de haute altitude ayant une capacité d'emport importante. La seule possibilité est le ballon-sonde météorologique, où tout est sacrifié: pas de nacelle, pas de moteur, pas de carburant, pas de lest, pas de soupape à gaz, pas d'ancre, enveloppe de gaz jetable, très fine, très fragile et très élastique qu'on laisse se distendre pour augmenter le volume et récupérer une partie de la perte de poussée d'Archimède en altitude. Ce genre de ballon parvient à monter à quelques dizaines de kilomètres. L'instabilité d'altitude qui résulte de l'élasticité de l'enveloppe n'est pas gênante pour cette application, le ballon étant à usage unique et son éclatement en fin de mission prévu.

La portance ne peut se piloter directement. Elle ne peut se piloter directement ni en direction, ni en sens, ni en intensité. On parvient cependant à commander l'altitude d'un ballon (tenant compte de l'inertie) en jouant avec:

- le lest (eau, sable...), plus lourd que l'air ;
- le gaz de sustentation, plus léger que l'air (quantité, température...).

Il faut bien entendu tenir compte des charges perdues en vol: carburant, bombes.


L'équilibre du ballon 


L'équation d'équilibre s'écrit: F = M.g

Equilibre du ballon


F: portance du paragraphe précédent [N]
O: point d'application de la portance F
M: masse du ballon [N]
G: centre de gravité, point d'application du poids M.g
A: métacentre de flottabilité
g: accélération due à la gravité (dirigée vers le bas) [m/s2]

L'altitude d'équilibre est celle pour laquelle la masse volumique de l'air réalise l'équation d'équilibre. La masse volumique de l'air (donc la portance) décroît en effet avec l'altitude.


Stabilité en vol 


         Stabilité de l'équilibre "poids-portance", ou stabilité d'altitude
     L'équilibre réalisé entre la portance et le poids du ballon est toujours stable, dès que le ballon se déforme suffisamment peu (en comparaison avec la compressibilité de l'air), pour présenter un volume pratiquement constant. On rappelle que la masse volumique de l'air ρ décroît avec l'altitude ; si le ballon a tendance à monter, ρ donc la poussée d'Archimède diminuent, et le ballon revient à son altitude d'équilibre.

     Ceci est toujours vrai (tissus ou structure métallique rigides), sauf pour certains ballons-sondes météorologiques. Mais ce n'est pas vrai avec les sous-marins dont la déformabilité de la coque n'est pas négligeable devant celle d'un liquide peu compressible comme l'eau, ce qui entraîne une instabilité en profondeur.


         Stabilité d'attitude
     Elle s'étudie comme pour les bateaux. On la réalise en plaçant G en toutes circonstances de vol et de chargement sous le(s) métacentre(s) de flottabilité A, ici presque confondu(s) avec O en raison du faible gradient de la masse volumique de l'air sur la hauteur totale du ballon.

     Il existe, comme pour les bateaux, un métacentre en tangage et un métacentre en roulis. Il faut donc étudier les deux cas. Le chargement de la quille des ballons résout pratiquement la question de la stabilité d'attitude, question nettement plus facile à résoudre que dans le cas des bateaux.


         Stabilité aérodynamique
     Cette stabilité n'intéresse que les dirigeables (les ballons libres ne se déplacent pas par rapport à l'air). Elle s'étudie comme pour celle d'un avion: stabilité en tangage, en lacet, en roulis. Elle s'obtient, comme pour un avion, en plaçant judicieusement le centre de gravité par rapport au(x) foyer(s) aérodynamique(s). On s'aide, comme pour un avion, de surfaces aérodynamiques appelées profondeur et dérive, pour la stabilité de tangage et celle de lacet.

     L'étude de la stabilité de roulis, pour un dirigeable, revient à l'étude de la stabilité d'attitude en roulis.

Contrôle du roulis avec une masse


Contrôle de l’altitude  




     Un dirigeable est un aéronef plus léger que l'air, celui-ci est constitué d'un ou de plusieurs ballonnets contenant du gaz (hélium ou hydrogène) dans le but de le soulever.
Le ballon est allongé pour être aérodynamique. Le lest, généralement du sable ou de l'eau, peut être lâché pour alléger l'appareil et gagner de l'altitude. A tout moment, on peut relâcher du gaz pour réduire la flottabilité, donc perdre de l'altitude. Pour diriger l'aéronef, le pilote utilise un ou plusieurs gouvernails articulés verticalement: pour commander la montée ou la descente, il actionne un ou plusieurs volets de profondeur articulés horizontalement.

Hélium
- Gaz rare (He) en quantité très faible sur Terre ;
- Donc très cher ;
- Léger (0,18 kg/m3 en conditions normales) ;
- Ininflammable, neutre à tous points de vue ;
- C'est le gaz actuellement le plus employé pour les ballons dirigeables ;
- Comme la molécule d'hélium est monoatomique et de très petite taille, le gaz se diffuse facilement à travers les parois (à l'échelle moléculaire, une paroi, c'est un grillage).


Hydrogène
- Elément très répandu sur Terre (2 millions de fois plus fréquent que l'hélium) ;
- Bon marché ;
- Molécule (H2) la plus légère (0,09 kg/m3) ;
- Le mélange avec l'air est inflammable dans de fortes proportions (la déflagration se propage à 10 m/s



Parois et structures  




Suivant la rigidité du ballon, la paroi contenant le gaz aura ou non le rôle de transmission mécanique des efforts pour soulever la charge utile, les moteurs, le carburant, etc.

Dans le type "ballon rigide", on dissocie en effet la fonction mécanique de la fonction "étanchéité au gaz". Cela permet de réaliser une structure mécanique avec les matériaux adaptés les plus légers (aluminium pour les Zeppelins, bois) avec une épaisseur convenable (moment d'inertie élevé pour obtenir la légèreté).

La fonction "paroi d'étanchéité au gaz" ne servant plus à "tenir" le ballon, elle peut se réaliser avec un matériau très léger qui se contente de transmettre l'effort statique du gaz de remplissage, localement, à la paroi rigide.



                                                            [retour à la page précédente]